The area of abed is 49 square units, a fundamental concept in geometry that measures the extent of a two-dimensional surface. Delving into the realm of area, this discourse unravels its mathematical representation, properties, and practical applications, offering a comprehensive understanding of this essential geometric concept.
From the area of simple shapes to complex polygons, the exploration unveils the nuances of area calculation, revealing its significance in diverse fields, from architecture to agriculture. With a blend of theoretical insights and real-world examples, this discourse illuminates the multifaceted nature of area, empowering readers with a deeper understanding of this foundational mathematical concept.
Definition of Area
In geometry, area is a quantitative measure representing the size of a two-dimensional surface. It is expressed in square units, such as square meters (m²), square centimeters (cm²), or square feet (ft²).
The area of a shape is determined by the number of unit squares that can fit within its boundaries. Different shapes have specific formulas for calculating their areas.
Examples of Area Formulas
- Square:Area = side length²
- Rectangle:Area = length × width
- Triangle:Area = (base × height) / 2
- Circle:Area = πr², where r is the radius
Properties of Area
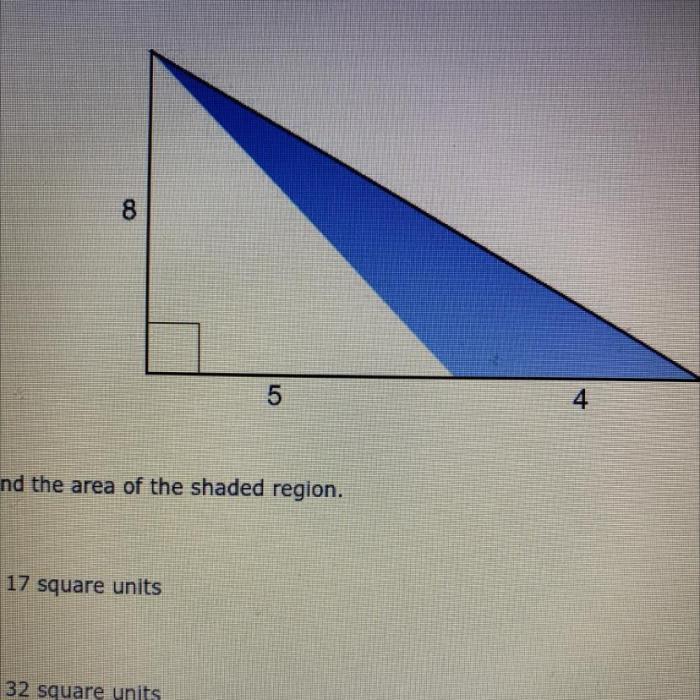
Area, a fundamental geometric property, possesses several notable characteristics. These properties are crucial for understanding the behavior of area in various geometric transformations and applications.
Additivity
Additivity is a key property of area, implying that the total area of a composite figure is equal to the sum of the areas of its individual components. For instance, if a rectangular plot of land has dimensions 10 meters by 20 meters, its area is 200 square meters.
If a circular garden with a radius of 5 meters is added to the plot, the total area becomes 200 + 25π square meters, where π represents the mathematical constant approximately equal to 3.14.
Invariance under Translation and Rotation
Area exhibits invariance under translation and rotation, meaning that it remains unchanged when a figure is moved or rotated without changing its shape. For example, if the rectangular plot mentioned earlier is shifted 5 meters to the right, its area remains 200 square meters.
Similarly, if the plot is rotated 90 degrees, its area stays the same.
Area of a Rectangle
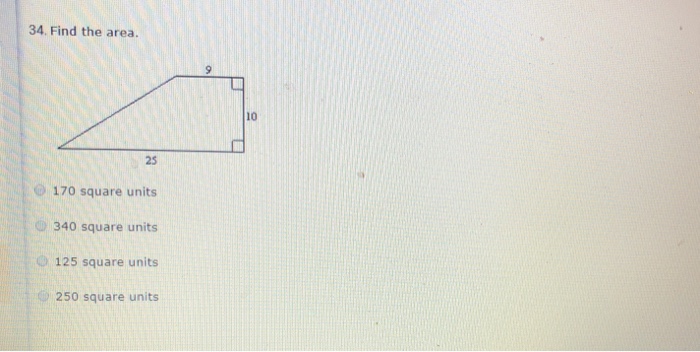
The area of a rectangle is the measure of the surface enclosed by its four sides. It is calculated by multiplying the length of the rectangle by its width. The formula for the area of a rectangle is:“`Area = length × width“`To find the area of a given rectangle, simply substitute the values of its length and width into the formula.
For example, if a rectangle has a length of 5 units and a width of 3 units, its area would be:“`Area = 5 units × 3 units = 15 square units“`
Properties of the Area of a Rectangle
The area of a rectangle has several important properties, including:
- The area of a rectangle is always positive.
- The area of a rectangle is additive. This means that the area of a larger rectangle can be found by adding the areas of its smaller sub-rectangles.
- The area of a rectangle is invariant under rotation. This means that the area of a rectangle does not change if it is rotated by any angle.
Perimeter and Area of a Rectangle: The Area Of Abed Is 49 Square Units
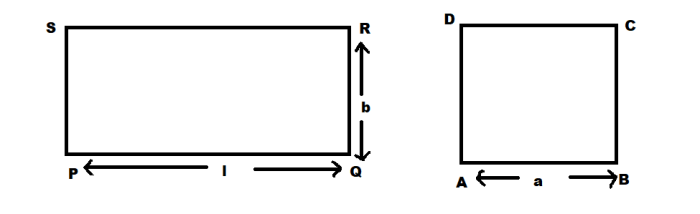
In geometry, a rectangle is a two-dimensional shape with four right angles. The length and width of a rectangle are the two dimensions that define its size. The perimeter of a rectangle is the sum of the lengths of all four sides, while the area is the measure of the surface enclosed by the rectangle.
Relationship between Perimeter and Area
The perimeter and area of a rectangle are related in the following way: the area of a rectangle is equal to the product of its length and width, while the perimeter is equal to twice the sum of its length and width.
Examples
Consider two rectangles with the same area of 49 square units. One rectangle has a length of 7 units and a width of 7 units, while the other rectangle has a length of 14 units and a width of 3.5 units.
- Rectangle 1:Length = 7 units, Width = 7 units, Perimeter = 2(7 + 7) = 28 units, Area = 7 – 7 = 49 square units
- Rectangle 2:Length = 14 units, Width = 3.5 units, Perimeter = 2(14 + 3.5) = 35 units, Area = 14 – 3.5 = 49 square units
As you can see, even though both rectangles have the same area, their perimeters are different. This is because the perimeter of a rectangle is dependent on the sum of its length and width, while the area is dependent on the product of its length and width.
Applications of Area

Area is a fundamental concept in geometry that measures the extent of a two-dimensional surface. It finds numerous practical applications in everyday life, across various fields such as architecture, engineering, and agriculture.
Architecture
In architecture, area plays a crucial role in designing and constructing buildings. Architects calculate the area of rooms, floors, and the entire building to determine the space available, plan layouts, and estimate material requirements.
Engineering, The area of abed is 49 square units
Engineers rely on area calculations for a wide range of projects. For example, in civil engineering, the area of a bridge or road is essential for determining the amount of materials needed and the structural integrity of the design. In mechanical engineering, the area of surfaces is crucial for calculating heat transfer, fluid flow, and other important parameters.
Agriculture
In agriculture, area is a critical factor in determining land use, crop yields, and resource allocation. Farmers calculate the area of their fields to plan crop rotation, estimate fertilizer and pesticide requirements, and assess potential crop yields.
Commonly Asked Questions
What is the definition of area?
Area is a mathematical concept that measures the extent of a two-dimensional surface, quantifying the amount of space it occupies.
How do you calculate the area of a rectangle?
The area of a rectangle is calculated by multiplying its length by its width, expressed as A = l × w.
What are the properties of area?
Area possesses several properties, including additivity, invariance under translation and rotation, and the property that congruent shapes have equal areas.